Let’s have a computer to play Mario Bros using reinforcement learning. In this experiment, we’ll attempt to teach a computer to master ‘Mario Bros’ using neural networks. Ready to level up?

Best attempt so far using a Double Deep Q Network (DDQN) after 29155 games

This article is an introduction on machine learning, neural network and reinforcment learning and how they interact. If you’re already familiar with these concepts feel free to jump ahead in the next articles:

Project introduction

Learning to play a game, such as Mario Bros, using neural networks, is a project I wanted to start for a long time. The machine learning field have always fascinated me. My PhD research focused on applying neural network to graphs, but the field of machine learning is remarkably vast. For example, I’ve never explored the world of reinforcement learning (RL).

In machine learning, there are three main ways to teach an algorithm:

  1. Supervised learning: this is the most intuitive method. It’s similar to teaching a child to recognise letters. For each letter they might encounter, you would say this is an 'A', this is a 'B', and so on. Technically you need to collect a labelised dataset: in this case, many letters occurences. For each letter you have to give it a label, sush as A, B, etc.

  2. Unsupervised learning: here, algorithms discover patterns on their own. Imagine children playing with shape-sorter toys. They figure out how to match shapes with the correct holes by focusing on key features like the shape, while ignoring irrelevant ones like color or material. Technically you let the algorithm create groups with data following the same patterns. Then you label each group afterward.

  3. Reinforcement learning: in this approach, an algorithm learns to perform tasks on its own by receiving rewards from the environment. This method seems to fit idealy in video games: each in-game action will result in a modification of the score, providing a reward, which guide the learning process to explore and exploit the game’s environment.

We’ve just talked about machine learning and neural networks, but what is the difference?

Neural networks and machine learning

Machine learning is a broad concept: it includes any algorithms that learn to solve a given task. In this context, ‘learning’ means adjusting the algorithm’s internal parameters.

Neural network are a type of learning algorithm inspired by biological neural networks1. They are usually structured in layers.

  • The first layer is the input: it’s where the data enters. For example, in a network designed to recognize letters from images, there’s a neuron for each pixel value.
  • The last layer is the ouput of the network. In the letter recognition example, there would be 26 output neurons. Each representing a different letter.
  • All the intermediate, or hidden, layers do the network’s computation.
  • Each neuron it connected with a certain strength, or weight, to some neurons in the next layer. The strengh is usually encoded between 0 (no connection) to 1 (full connection). See the next figure, where the weights are indicated in red on each connection.
  • A neuron receives an activation level (a value) and propagate its activation, given the strength of the connections, to the next neurons.

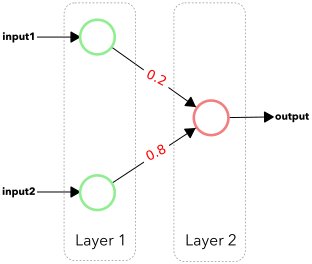Activation propagation Simplified activation propagation: the layer 1 neurons, in green, receive an activation, noted inputs. This activations passe througt the connections to the layer 2 neuron, in orange. This neuron’s activation is its output. Here, he values in red, in the middle of the connections represent their weights (their strength). The output neuron activation computation is quite simple: if the inputs are 1.0 and 0.5, it’s activation will be 0.6 ($= 1.0 \times 0.2 + 0.5 \times 0.8$)2.

  • Learning occurs through a process called error backpropagation, which alter the strenght of connections (the red values). This process turns on or off each neuron’s activation on the following neurons. We’ve said in machine learning, we are adjusting some internal values of the algorithm. In neural network we specifically adjust the weights of the connections.

  • The error is the difference between the output of the network and the labels we already know. In the letter recognition example, we have 26 output neurons. If we present an A and the network output is 0 for all output neurons except the first one, we considere the network is right. On the opposite, if all the outputs are 0, except the second one (that should be activated only for the letter B). This is an error. In this case, the backpropagation will alter all network’s connections to tend to the right answer on the next trial.

  • On a side note, we like networks answers to be values between 0 and 1 for each neurons. That’s why we use activation functions at the end of layers. In our example, on the output layer, we’d like the ouput to be as closer as possible to 0 or 1. But what if the values are less close like 0.3 or 0.8? Some activation function, like softmax, tends to ‘push’ mean values to 0 and 1. So we likely use such function a the end of our output layer. Designing neural networks can be challenging.

After this overview of neural networks, you can understand how they work: information is feeded to the input layer, transformed by each layers neurons and connections and a result is given as the activation of the last layer. After an error, the backpropagation try to correct the connections.

Beside being composed of very simple units (neurons and connections), neural networks are powerful: they have the ability to approximate any function3. I like to see them as compressed look-up tables, storing experiences, making them ideal to create estimators or mapping functions in large space.

But how can neural networks be used in reinforcement learning?

Reinforcement Learning

Reinforcement Learning (RL) is a method of machine learning where an agent learns decision-making in an environment to achieve a goal. Unlike traditional methods used for classification or prediction, RL focuses on learning a strategy, or policy, to take actions based on environmental feedback.

  • Agent: The algorithm that learns and makes decisions. For instance, in chess, it can be the algorithm playing one of the two sides.

  • Environment: What the agent interacts with. It can provide rewards in response to the agent’s actions. In the chess analogy, this includes the chess framework and the board. A reward might be given for capturing an opposing piece or expanding ground control.

  • State: A snapshot of the environment at a specific time. Example: the arrangement of pieces on a chessboard at a given moment. The state space is the range of possible arrangements the environment can have. While it can be extremelly vast in chess (all the possible combination of the pieces on the board) or in Go. On the opposite, in games like tic-tac-toe, it is very limited.

  • Action: The agent’s input to the environment. In chess, this could be moving a pawn to B3. The action space is the range of possible actions the agent can choose from. While it can be vast in chess, in games like Tetris, it is very limited: move left, move right, rotate left, rotate right, and move down at each frame.

  • Reward: A value provided by the environment (or computed from the state) indicating the positivity of an action. This can be challenging to compute or apply. For example, in chess, you might use a value function to interpret and reward actions (e.g., capturing a rook is worth 5 points, checkmating the king is worth 10 points). In video games, the score is often used as part of the reward.

  • Value function: A function that compute a reward for a given state. The action-value function is a variation of this function, that returns an estimated reward for a given state-action pair. For example, in chess, when in check, an action leading to checkmate is more valuable than one that merely expands ground control.

  • Policy: A function that maps states to actions. For an agent, it can be a strategy like “when I see this state, I do that.” In chess, a policy might be to move the king out of check when detected.

In RL problems, states and action space can be complex and high-dimensional (like in the chess game). It is fairly impossible for a human to write what action an agent has to take given the board state, like a look-up table, that store the ideal action given any state.

In an ideal world, we’d like this look-up table to be compact and discovered by the agent instead of written by humans. That’s where neural networks enter in the game. We’ve seen they are universal approximators that act like a compressed look-up table. In fact we can use neural network at different points in RL:

  • As a policy: a neural network compute or store directly the action to take given the state. It will act as a state-action look-up table.
  • As a value function: as an estimator that compute the reward for a given state.
  • As a compressor: when states or actions spaces can be very large, we might want a neural network to compress, by computing a represention (another interesting property of neural networks), into a smaller space. This can be combined with the two previous strategies.

Why this this challenging?

The core challenge in RL is how effectively assign rewards to a sequence of actions leading to a delayed outcome. In many scenarios, the ultimate reward is only known at the end of a sequence of actions, such as winning or losing a chess game. The challenge involves determining how to backpropagate the final reward to earlier actions, optimizing the agent’s policy (its decision-making strategy) to favor actions that are more likely to lead to successful outcomes in the long run.

The video shown at the top of the page is a good episode, but it doesn’t mean the model has converged to a state where it plays only good episodes.

My goal with this project is to deepen my understanding of reinforcement learning and its algorithms, and to share about what I learnt. I’d like to see if a computer can truly master ‘Mario Bros’ through these methods.

Next steps

Thank you for reading this long and technical article. I tried to explain all our challenges and the tools we can use.

In the upcoming articles, we’ll talk about the setup to play ‘Mario Bros’ and experiment with algorithms like Double Deep Q Networks (DDQN), Proximal Policy Optimization (PPO, which is interesting because it’s the algorithm behind RL from Human Feedback (RLHF) used to train the GPT models) and probably NeuroEvolution of Augmenting Topologies (NEAT, which is not an reinforment learning algorithm, as it doesn’t use the error retropropagation, but seems cool and very efficient).

Stay tuned for the next article we’ll discuss about the project setup.

Thanks again for your time and see you!

  1. Original model from McCulloch and Pitts: Warren S. MCCULLOCH and Walter PITTS. «A logical calculus of the ideas immanent in nervous activity». In: The bulletin of mathematical biophysics 5.4 (1943), p. 115-133. ISSN: 1522-9602. DOI: 10.1007/BF02478259. ↩

  2. More formally, the output $y$ of a neuron is given by $y = \sigma(b + \sum_{i \in I} w_i . x_i)$, where $I$ is the set of the input neurons, $x_i$ is the activation of the input neuron $i$, $w_i$ is the weigth of the connection between $i$ and the current neuron, $b$ is the bias (a value representing prior knowledge on the task) of the current neuron and $\sigma$ is an activation function. ↩

  3. They are referred as universal approximators: Kurt HORNIK. «Approximation capabilities of multilayer feedforward networks». In: Neural Networks 4.2 (1991), p. 251-257. ISSN: 08936080. DOI: 10.1016/0893-6080(91)90009-T. ↩